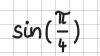Difference between revisions of "Eindimensionale Eingabe"
(→Beispiele) |
m (→Beispiele) |
||
| Line 42: | Line 42: | ||
| { (x,y) in RR^2 : 1<=x<=2, -x <= y <= 1+x^2} || [[File:example07.png|100px]] || \( \left\{ (x,y) \in \mathbb{R}^2 : 1 \le x \le 2, -x \le y \le 1+x^2 \right\} \) | | { (x,y) in RR^2 : 1<=x<=2, -x <= y <= 1+x^2} || [[File:example07.png|100px]] || \( \left\{ (x,y) \in \mathbb{R}^2 : 1 \le x \le 2, -x \le y \le 1+x^2 \right\} \) | ||
|- | |- | ||
| − | | { ( | + | | LL = { (1,2,-1,3)^T + t (1,-1,2,-1) : t in RR } || [[File:example08.png|100px]] || \( \mathbb{L} = \big\{ (1,2,-1,3)^T + t \; (1,-1,2,-1) : t \in \mathbb{R} \big\} \) |
|- | |- | ||
| − | | | + | | 90^o - 30^o || [[File:example09.png|100px]] || \( 90^\circ - 30^\circ \) |
|- | |- | ||
| − | | | + | | (-oo,-1) uu [2,oo)|| [[File:example10.png|100px]] || \( ( -\infty, -1) \cup [2,\infty) \) |
|- | |- | ||
| − | | | + | | a != 2 => L = {1/2}|| [[File:example11.png|100px]] || \( a \neq 2 \Rightarrow L = \left\{ \frac{1}{2} \right\} \) |
|- | |- | ||
| − | | | + | | (-2,3) nn (3,4) = {} || [[File:example12.png|100px]] || \( (-2,3) \cap (3,4) = \{\} \) |
|- | |- | ||
| − | | ( | + | | g : vec(x) = vec(p) + t vec(a), t in RR || [[File:example13.png|100px]] || \( g: \vec{x} = \vec{p} + t \vec{a}, t \in \mathbb{R} \) |
|- | |- | ||
| − | | | + | | 2 x_1 - 4 x_2 + 5 x_3 = -7 || [[File:example14.png|100px]] || \( 2 x_1 - 4 x_2 + 5 x_3 = -7 \) |
|- | |- | ||
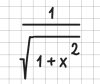
| − | | 2 | + | | int 1/(1+x^2) dx = arctan(x) + C, C in RR || [[File:example15.png|100px]] || \( \displaystyle \int \frac{1}{1+x^2} \, dx = \arctan(x) + C, C \in \mathbb{R} \) |
|- | |- | ||
| − | + | | ln |x-1| || [[File:example16.png|100px]] || \( \ln(| x-1 |) \) | |
| − | |||
| − | | ln |x-1| || [[File: | ||
|} | |} | ||
Revision as of 18:41, 29 October 2022
Allgemeine Hinweise
Mathematische Ausdrücke werden als reiner Ascii-Text, also ohne Sonderzeichen, eingegeben, So liefert etwa pi den griechischen Buchstaben \( \pi \).
Wir verwenden implizite Multiplikation, d.h. ein Leerzeichen zwischen zwei Bezeichnern wirkt als Multiplikation: a*b liefert das gleiche Ergebnis wie a b. Ohne Leerzeichen wird der Ausruck allerdings als eigenständiger; Bezeichner ab betrachtet.
Erkannte Funktionen werden in einem speziellen Font dargestellt:
sin(x) liefert \( \sin(x) \), sinc(x) liefert hingegen \( sinc(x) \).
Bei manchen Aufgaben ist die Lösung die leere Menge. Diese wird durch {} dargestellt.
Beispiele
Bezeichner und Operatoren
| \( \alpha \): alpha | \( \beta \): beta | \( \gamma \): gamma | \( \delta \): delta | \( \epsilon \): epsilon | \( \zeta \): zeta |
| \( \eta \): eta | \( \vartheta \): theta | \( \iota \): iota | \( \kappa \): kappa | \( \lambda \): lambda | \( \mu \): mu |
| \( \nu \): nu | \( \xi \): xi | \( \pi \): pi | \( \varrho \): rho | \( \sigma \): sigma | \( \tau \): tau |
| \( \varphi \): phi | \( \chi \): chi | \( \psi \): psi | \( \omega \): omega | \( \Omega \): Omega | |
| \( \infty \): oo | \( \in \): in | \( ^\circ \): ^o | \( ^\top \): ^T | \( \cup \): uu | \( \cap \): nn |
| \( \mathbb{N} \): NN | \( \mathbb{Z} \): ZZ | \( \mathbb{Q} \): QQ | \( \mathbb{R} \): RR | \( \mathbb{C} \): CC | \( \mathbb{L} \): LL |
| \( \le \): <= | \( \ge \): >= | \( \neq \): != | \( \Rightarrow \): => | \( \Leftrightarrow \): <=> |
Funktionen
arccos, arccosh, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, det, exp,
ln, log, sin, sinh, sqrt, tan, tanh, abs, min, max, vec