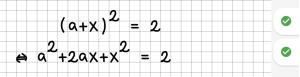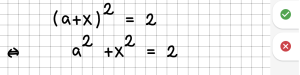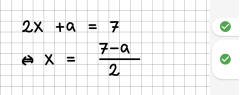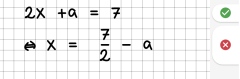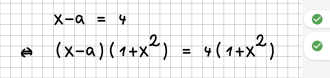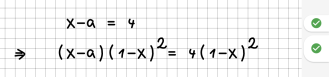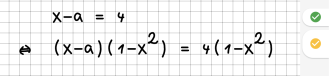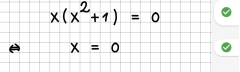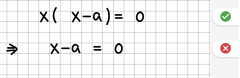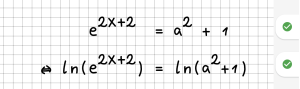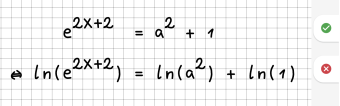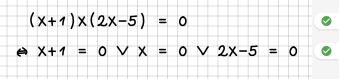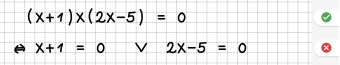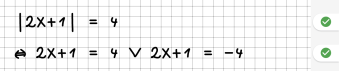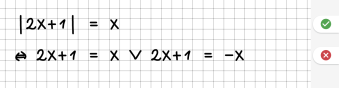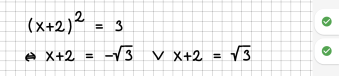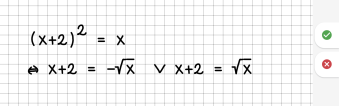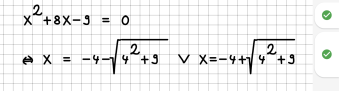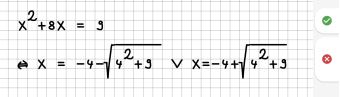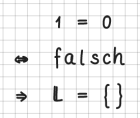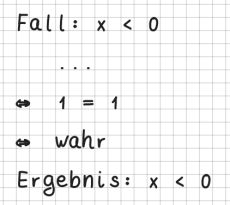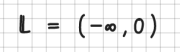Difference between revisions of "Herleitungsaufgaben"
Sven.guyet (talk | contribs) (Created page with "<p>Bei Herleitungsaufgaben (nur im 2D-Format) besteht das Ziel darin, die Lösung ausgehend von der Aufgabenstellung schrittweise herzuleiten, damit das System (welches das En...") |
Sven.guyet (talk | contribs) |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | == Herleitungen == | ||
| + | |||
<p>Bei Herleitungsaufgaben (nur im 2D-Format) besteht das Ziel darin, die Lösung ausgehend von der Aufgabenstellung schrittweise herzuleiten, damit das System (welches das Endergebnis übrigens nicht kennt) Ihnen folgen kann und am Ende Ihr Ergebnis akzeptiert.</p> | <p>Bei Herleitungsaufgaben (nur im 2D-Format) besteht das Ziel darin, die Lösung ausgehend von der Aufgabenstellung schrittweise herzuleiten, damit das System (welches das Endergebnis übrigens nicht kennt) Ihnen folgen kann und am Ende Ihr Ergebnis akzeptiert.</p> | ||
| − | <p>Hierzu müssen Sie zunächst mit einer bekannten Aussage (aus der Aufgabenstellung) starten. Nun können Sie die gegebene Gleichung oder Ungleichung solange umformen, bis Sie zu einem Endergebnis gelangt sind. Wichtig ist dabei, dass das System erkennen kann, wie zwei aufeinanderfolgende (Un)Gleichungen miteinander in Verbindung stehen. Dies wird durch das Äquivalenzzeichen | + | <p>Hierzu müssen Sie zunächst mit einer bekannten Aussage (aus der Aufgabenstellung) starten. Nun können Sie die gegebene Gleichung oder Ungleichung solange umformen, bis Sie zu einem Endergebnis gelangt sind. Wichtig ist dabei, dass das System erkennen kann, wie zwei aufeinanderfolgende (Un)Gleichungen miteinander in Verbindung stehen. Dies wird durch das Äquivalenzzeichen ⇔ oder den Folgepfeil ⇒ angezeigt. Fehlt diese Verknüpfung, so wird angenommen, dass es sich um eine bereits bekannte Aussage handelt, und die Aufgabenstellung wird danach durchsucht. Wird nichts passendes gefunden, wertet das System die Zeile als Fehler und zeigt dies entsprechend an.</p> |
| + | |||
| + | <p>Aus technischen Gründen (auch in Bezug auf Rückmeldungen) darf pro Zeile immer nur eine Gleichung stehen.</p> | ||
| − | <p> | + | <p>Das System erkennt mit Stand Januar 2023 die folgenden Umformungen:</p> |
{| class="wikitable" style="margin-left: 0px; margin-right: auto;" | {| class="wikitable" style="margin-left: 0px; margin-right: auto;" | ||
| Line 11: | Line 15: | ||
! style="text-align:left;"| Fehler | ! style="text-align:left;"| Fehler | ||
|- style="vertical-align:top;" | |- style="vertical-align:top;" | ||
| − | | 1 || Eine Gleichung wird nur umgestellt. || || | + | | 1 || Eine Gleichung wird nur umgestellt. |
| − | |- | + | | [[File:Regel01.png|300px]] || [[File:Fehler01.png|300px]] |
| − | | 2 || Eine Gleichung wird mit einer Konstanten multipliziert, und evtl. werden noch Terme auf beiden Seiten addiert. | || | + | |- style="vertical-align:top;" |
| − | |- | + | | 2 || Eine Gleichung wird mit einer Konstanten multipliziert, und evtl. werden noch Terme auf beiden Seiten addiert. |
| + | | [[File:Regel02.png|240px]] || [[File:Fehler02.png|240px]] | ||
| + | |- style="vertical-align:top;" | ||
| 3 || Eine Gleichung wird mit einem Term multipliziert, der (evtl.) Null sein kann. | | 3 || Eine Gleichung wird mit einem Term multipliziert, der (evtl.) Null sein kann. | ||
| − | | || | + | | [[File:Regel03.png|330px]]<br /> |
| − | |- | + | Der Term (1+x^2) kann nicht Null sein, daher ist dies eine Äquivalenzumformung.<br /> |
| + | [[File:Regel03b.png|330px]]<br /> | ||
| + | Da 1-x^2 Null sein kann, ist dies nur eine Implikation. | ||
| + | | [[File:Fehler03.png|330px]]<br /> | ||
| + | Der Term (1-x^2) kann Null sein, daher ist dies keine Äquivalenzumformung. | ||
| + | |- style="vertical-align:top;" | ||
| 4 || Eine Gleichung wird durch einen Term geteilt, der nie Null sein kann. | | 4 || Eine Gleichung wird durch einen Term geteilt, der nie Null sein kann. | ||
| − | | || | + | | [[File:Regel04.png|240px]]<br /> |
| − | |- | + | Der Term x^2 +1 kann niemals Null sein, daher können wir die Gleichung dadurch teilen. |
| + | | [[File:Fehler04.png|240px]]<br /> | ||
| + | Hier wird durch einen Term geteilt, der Null sein kann. Daher ist dies auch keine Implikation mehr; wir verlieren hier mögliche Lösungen. | ||
| + | |- style="vertical-align:top;" | ||
| 5 || Es wird eine Funktion auf beide Seiten angewendet (quadrieren, Wurzel, Exponentialfunktion, Logarithmus, trigonometrische Funktionen, ...). | | 5 || Es wird eine Funktion auf beide Seiten angewendet (quadrieren, Wurzel, Exponentialfunktion, Logarithmus, trigonometrische Funktionen, ...). | ||
| − | | || | + | | [[File:Regel05.png|300px]] || [[File:Fehler05.png|340px]]<br /> |
| − | |- | + | Die Funktion wird immer auf die komplette rechte und linke Seite angewendet, nicht auf einzelne Summanden! |
| + | |- style="vertical-align:top;" | ||
| 6 || Nullstellen werden faktorisiert. | | 6 || Nullstellen werden faktorisiert. | ||
| − | | || | + | | [[File:Regel06.png|340px]] || [[File:Fehler06.png|340px]]<br /> |
| − | |- | + | Hier wurde eine Nullstelle verloren. |
| + | |- style="vertical-align:top;" | ||
| 7 || Beträge können aufgelöst werden:<br /> | | 7 || Beträge können aufgelöst werden:<br /> | ||
&vbar;f(x)&vbar; = g(x)<br /> | &vbar;f(x)&vbar; = g(x)<br /> | ||
<=> f(x) = -g(x) v f(x) = g(x),<br /> | <=> f(x) = -g(x) v f(x) = g(x),<br /> | ||
falls g(x) immer größer oder gleich Null ist. | falls g(x) immer größer oder gleich Null ist. | ||
| − | | || | + | | [[File:Regel07.png|340px]] || [[File:Fehler07.png|340px]]<br /> |
| − | |- | + | x kann auch negativ sein. |
| + | |- style="vertical-align:top;" | ||
| 8 || Quadratische Gleichungen können aufgelöst werden:<br /> | | 8 || Quadratische Gleichungen können aufgelöst werden:<br /> | ||
f(x)^2 = g(x)<br /> | f(x)^2 = g(x)<br /> | ||
<=> f(x) = -sqrt(g(x)) v f(x) = sqrt(g(x)),<br /> | <=> f(x) = -sqrt(g(x)) v f(x) = sqrt(g(x)),<br /> | ||
falls g(x) immer größer oder gleich Null ist. | falls g(x) immer größer oder gleich Null ist. | ||
| − | | || | + | | [[File:Regel08.png|340px]] || [[File:Fehler08.png|340px]]<br /> |
| − | |- | + | Rechte Seite kann negativ sein. |
| + | |- style="vertical-align:top;" | ||
| 9 || Ansatzweise wird auch die pq-Formel erkannt. | | 9 || Ansatzweise wird auch die pq-Formel erkannt. | ||
| − | | || | + | | [[File:Regel09.png|340px]] || [[File:Fehler09.png|340px]]<br /> |
| − | | | + | Die Gleichung war noch nicht in der Form <br>x^2 + px + q = 0. |
| + | |} | ||
| + | |||
| + | <p>Ist eine Gleichung immer erfüllt, dann hat diese den Wert <q>wahr</q>, also z.B. 1 = 1 <=> wahr.</p> | ||
| + | <p>Ist eine Gleichung nie erfüllt, dann hat diese den Wert <q>falsch</q>, also z.B. 1 = 0 <=> falsch.</p> | ||
| + | |||
| + | [[#toc|→ Kapitelübersicht]] [[Main Page|→ Hauptseite]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<!-- *********************************************************** --> | <!-- *********************************************************** --> | ||
<!-- *********************************************************** --> | <!-- *********************************************************** --> | ||
<!-- *********************************************************** --> | <!-- *********************************************************** --> | ||
| − | + | == Endergebnis == | |
| − | + | <p>Das Endergebnis wird in der Form <q>''LL = ...''</q> dargestellt. Ist eine Gleichung nie lösbar, so kann dies folgendermaßen beschrieben werden:</p> | |
| − | <p>Das Endergebnis wird in der Form < | + | ...<br /> |
| − | ...<br> | + | |
| − | + | [[File:Endergebnis.png|140px]] | |
| + | |||
| + | [[#toc|→ Kapitelübersicht]] [[Main Page|→ Hauptseite]] | ||
| + | |||
<!-- *********************************************************** --> | <!-- *********************************************************** --> | ||
<!-- *********************************************************** --> | <!-- *********************************************************** --> | ||
<!-- *********************************************************** --> | <!-- *********************************************************** --> | ||
| − | + | == Fallunterscheidungen == | |
| − | + | ||
| − | <p>Fälle werden durch die Markierung < | + | <p>Fälle werden durch die Markierung <q>''Fall: Bedingung''</q> eingeleitet und mit |
| − | + | <q>''Ergebnis: Bedingung''</q> abgeschlossen. Das für diesen Fall gültige Zwischenergebnis ergibt sich aus der letzten Äquivalenzumformung oder Folgerung unterhalb des Falls. Die Bedingung muss immer in expliziter Form vorliegen, d.h. nach einer Variablen aufgelöst sein. So ist z.B. <q>''x > 1/2''</q> eine gültige Bedingung, | |
| − | Variablen aufgelöst sein. | + | <q>''2x > 1''</q> hingegen nicht.</p> |
| − | <p>Das Zwischenergebnis muss eine Bedingung bzw. Gleichung oder Ungleichung (keine Menge!) sein. Im folgenden Beispiel gibt es für den Fall, dass x > 0 ist, keine Lösung:</p> | + | |
| − | + | <p>Das Zwischenergebnis muss eine Bedingung bzw. Gleichung oder Ungleichung (also keine Menge!) sein. Im folgenden Beispiel gibt es für den Fall, dass x > 0 ist, keine Lösung:</p> | |
| − | <p>Hingegen ist im nächsten Beispiel für den Fall, dass x < 0 ist, jeder Wert eine Lösung:</p> | + | |
| − | + | [[File:Fall-falsch.png|230px]] | |
| − | <p>Wird eine Fallunterscheidung durchgeführt, so muss am Ende ein Gesamtergebnis in der Form < | + | |
| − | + | <p>Hingegen ist im nächsten Beispiel für den Fall, dass x < 0 ist, jeder Wert eine Lösung:</p> | |
| + | |||
| + | [[File:Fall-wahr.png|230px]] | ||
| + | |||
| + | <p>Wird eine Fallunterscheidung durchgeführt, so muss am Ende ein Gesamtergebnis in der Form <q>''LL = ...''</q> angegeben werden.</p> | ||
| + | |||
| + | [[File:Loesung.png|180px]] | ||
| + | |||
| + | [[#toc|→ Kapitelübersicht]] [[Main Page|→ Hauptseite]] | ||
| + | |||
| + | <!-- *********************************************************** --> | ||
| + | == Erkannte Regeln == | ||
| + | |||
| + | <p>Bei Herleitungsaufgaben versucht das System versucht, den Lösungsweg nachzuvollziehen. Die dabei angewandten | ||
| + | (hinterlegten) Regeln finden Sie auf der Seite '''[[Hinterlegte Regeln]]'''.</p> | ||
| + | |||
| + | [[#toc|→ Kapitelübersicht]] [[Main Page|→ Hauptseite]] | ||
Latest revision as of 19:25, 6 April 2023
Herleitungen
Bei Herleitungsaufgaben (nur im 2D-Format) besteht das Ziel darin, die Lösung ausgehend von der Aufgabenstellung schrittweise herzuleiten, damit das System (welches das Endergebnis übrigens nicht kennt) Ihnen folgen kann und am Ende Ihr Ergebnis akzeptiert.
Hierzu müssen Sie zunächst mit einer bekannten Aussage (aus der Aufgabenstellung) starten. Nun können Sie die gegebene Gleichung oder Ungleichung solange umformen, bis Sie zu einem Endergebnis gelangt sind. Wichtig ist dabei, dass das System erkennen kann, wie zwei aufeinanderfolgende (Un)Gleichungen miteinander in Verbindung stehen. Dies wird durch das Äquivalenzzeichen ⇔ oder den Folgepfeil ⇒ angezeigt. Fehlt diese Verknüpfung, so wird angenommen, dass es sich um eine bereits bekannte Aussage handelt, und die Aufgabenstellung wird danach durchsucht. Wird nichts passendes gefunden, wertet das System die Zeile als Fehler und zeigt dies entsprechend an.
Aus technischen Gründen (auch in Bezug auf Rückmeldungen) darf pro Zeile immer nur eine Gleichung stehen.
Das System erkennt mit Stand Januar 2023 die folgenden Umformungen:
Ist eine Gleichung immer erfüllt, dann hat diese den Wert wahr
, also z.B. 1 = 1 <=> wahr.
Ist eine Gleichung nie erfüllt, dann hat diese den Wert falsch
, also z.B. 1 = 0 <=> falsch.
→ Kapitelübersicht → Hauptseite
Endergebnis
Das Endergebnis wird in der Form LL = ...
dargestellt. Ist eine Gleichung nie lösbar, so kann dies folgendermaßen beschrieben werden:
...
→ Kapitelübersicht → Hauptseite
Fallunterscheidungen
Fälle werden durch die Markierung Fall: Bedingung
eingeleitet und mit
Ergebnis: Bedingung
abgeschlossen. Das für diesen Fall gültige Zwischenergebnis ergibt sich aus der letzten Äquivalenzumformung oder Folgerung unterhalb des Falls. Die Bedingung muss immer in expliziter Form vorliegen, d.h. nach einer Variablen aufgelöst sein. So ist z.B. x > 1/2
eine gültige Bedingung,
2x > 1
hingegen nicht.
Das Zwischenergebnis muss eine Bedingung bzw. Gleichung oder Ungleichung (also keine Menge!) sein. Im folgenden Beispiel gibt es für den Fall, dass x > 0 ist, keine Lösung:
Hingegen ist im nächsten Beispiel für den Fall, dass x < 0 ist, jeder Wert eine Lösung:
Wird eine Fallunterscheidung durchgeführt, so muss am Ende ein Gesamtergebnis in der Form LL = ...
angegeben werden.
→ Kapitelübersicht → Hauptseite
Erkannte Regeln
Bei Herleitungsaufgaben versucht das System versucht, den Lösungsweg nachzuvollziehen. Die dabei angewandten (hinterlegten) Regeln finden Sie auf der Seite Hinterlegte Regeln.