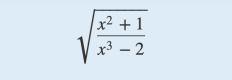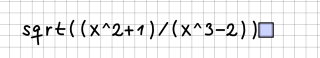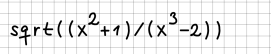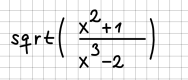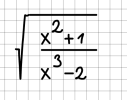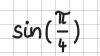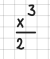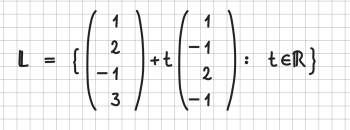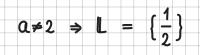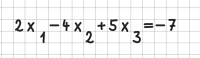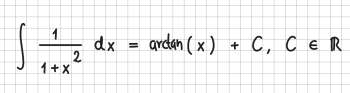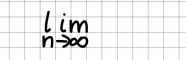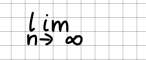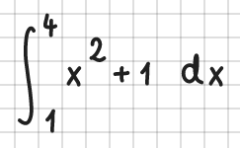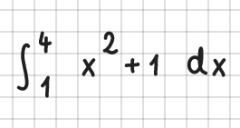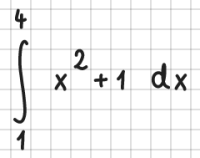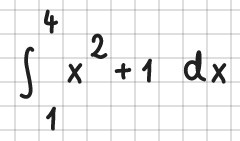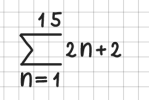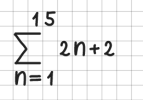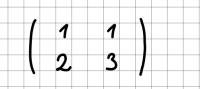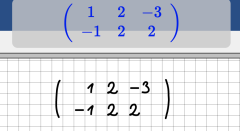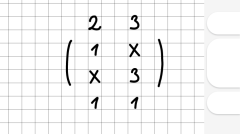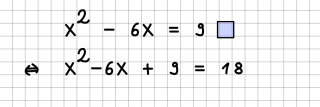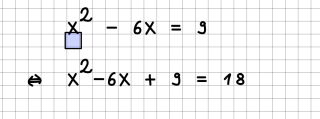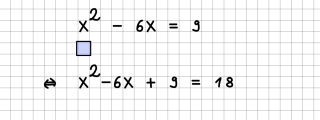Zweidimensionale Eingabe

Einleitung

Beim 2D-Format erfolgt die mathematische Eingabe in einem zweidimensionalen Kästchenraster (Eingabebereich mit beliebig vielen Zeilen und Spalten, vergleichbar mit einem karierten Blatt). Potenzen, Indizes, Brüche, Wurzeln und andere mathematische Konstrukte können Sie hier wie bei Verwendung von Stift und Papier durch Ausnutzung der Rasters in zweidimensionaler Form schreiben; siehe hierzu Abschnitt Beispiele.

Es wird grundsätzlich implizite Multiplikation verwendet, d.h. ein Leerzeichen zwischen zwei Bezeichnern wirkt als Multiplikation: a*b liefert somit dasselbe Ergebnis wie a b. Ohne Leerzeichen wird der Ausdruck allerdings als eigenständiger Bezeichner ab betrachtet.

Für mathematische Bezeichner, Operatoren und Sonderzeichen sind bestimmte Zeichenfolgen zu verwenden, die nach Eingabe eines Leerzeichens oder einer Klammer interpretiert und durch das entsprechende Symbol ersetzt werden. So liefert etwa pi den griechischen Buchstaben \( \pi \). Eine vollständige Liste unterstützter Symbole ist im Abschnitt Sonderzeichen und griechische Buchstaben aufgeführt.

Mathematische Funktionen werden nach Eingabe eines Leerzeichens oder einer Klammer speziell dargestellt. Der Abschnitt Funktionen enthält die Übersicht der erkannten und unterstützten Funktionen. Im Anschluss daran finden sich weitere Informationen zu darüber hinausgehenden mathematischen Ausdrücken wie Wurzeln, Grenzwerte oder Matrizen.

Bei manchen Aufgaben ist die gesuchte Lösung die leere Menge. Diese wird durch {} dargestellt.

→ Kapitelübersicht  → Hauptseite

Beispiele

Angenommen, wir wollen den folgenden Ausdruck aufschreiben:

Dies kann in der (eindimensionalen) Form sqrt( (x^2+1)/(x^3-2)) erfolgen, indem wir diese 1:1 ins Kästchenraster eintragen:

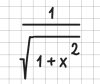
Wir können aber auch ausnutzen, dass wir im 2D-Format weitere Zeilen zur Verfügung haben und somit Exponenten auch durch Höhersetzen darstellen werden können:

Wir können den Bruch aber auch als Bruch schreiben:

Und schließlich können wir statt sqrt auch das Wurzelzeichen verwenden:

Wichtig: In jedem Kästchen kann jeweils nur ein Zeichen stehen.

Mathematischer Ausdruck	2D-Eingabe
\( (a + b)^2 \)
\( \sin \left( \frac{\pi}{4} \right) \)
\( a^2 + 2 a \, b + b^2 \)
\( \frac{1}{\sqrt{1+x^2}} \)
\( \frac{x^3}{2} \)
\( x^{\frac{3}{2}} \)
\( \left\{ (x,y) \in \mathbb{R}^2 : 1 \le x \le 2, -x \le y \le 1+x^2 \right\} \)
\( \mathbb{L} = \big\{ (1,2,-1,3)^T + t \; (1,-1,2,-1) : t \in \mathbb{R} \big\} \)
\( 90^\circ - 30^\circ \)
\( ( -\infty, -1) \cup [2,\infty) \)
\( a \neq 2 \Rightarrow L = \left\{ \frac{1}{2} \right\} \)
\( (-2,3) \cap (3,4) = \{\} \)
\( g: \vec{x} = \vec{p} + t \vec{a}, t \in \mathbb{R} \)
\( 2 x_1 - 4 x_2 + 5 x_3 = -7 \)
\( \displaystyle \int \frac{1}{1+x^2} \, dx = \arctan(x) + C, C \in \mathbb{R} \)
\( \ln(| x-1 |) \)

→ Kapitelübersicht  → Hauptseite

Sonderzeichen und griechische Buchstaben

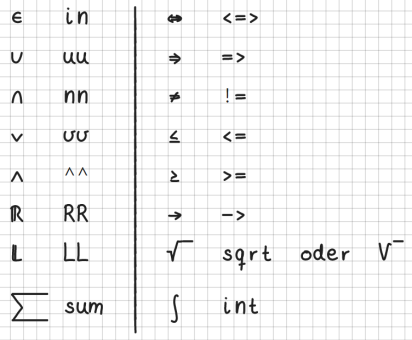
Bei den Sonderzeichen orientieren wir uns an der asciiMath Notation:

Griechische Buchstaben werden ausgeschrieben. Dabei orientieren wir uns an der englischen Schreibweise:

→ Kapitelübersicht  → Hauptseite

Funktionen

Folgende Funktionen werden aktuell erkannt:

exp	e-Funktion		sin	Sinus		arcsin	Arkussinus
ln	Natürlicher Logarithmus		sinh	Cosinus		arsinh	Areasinus hyperbolicus
log	Logarithmus		cos	Cosinus		arccos	Arkuscosinus
sqrt	Wurzel		cosh	Cosinus hyperbolicus		arcosh	Areacosinus hyperbolicus
abs	Betrag		tan	Tangens		arctan	Arkustangens
max	Maximum		tanh	Tangens hyperbolicus		artanh	Areatangens hyperbolicus
min	Minimum		cot	Cotangens		arccot	Arkuscotangens
det	Determinante		coth	Cotangens hyperbolicus		arcoth	Areacotangens hyperbolicus
vec	Vektor		coth	Cotangens hyperbolicus		arcoth	Areacotangens hyperbolicus

→ Kapitelübersicht  → Hauptseite

Nutzereinstellungen

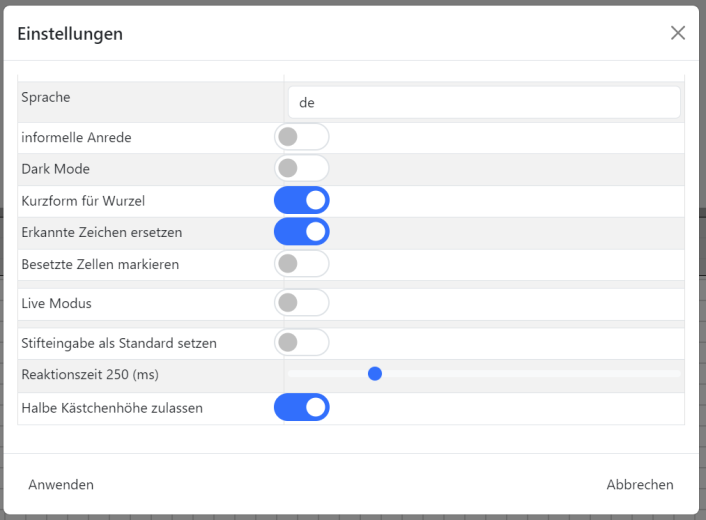
Über das Zahnradsymbol unten rechts können Sie allgemeine Nutzereinstellungen für die 2D-Eingabe vornehmen:

Die einzelnen Angaben haben folgende Bedeutung:

• informelle Anrede: Hier können Sie zwischen einer formalen und einer persönlichen Form wählen.
• Dark Mode: Dunkler Hintergrund
• Kurzform für Wurzel: V- und Leerzeichen wird zu einem Wurzelzeichen. (Empfehlung: Einschalten)
• Erkannte Zeichen ersetzen: Sonderzeichen werden durch das entsprechende Symbol ersetzt. (Empfehlung: Einschalten)
• Besetzte Zeichen markieren: Die Zellen, die von einem Zeichen besetzt werden, werden farblich hervorgehoben. (Empfehlung: Ausschalten)
• Live Modus: Ist dieser aktiviert, wo wird das vorherige Zeichen bearbeitet, sobald man im nächsten Kästchenfeld etwas schreibt. Ist der Live Modus inaktiv, so wird gewartet, bis in der vorgegebenen Reaktionszeit keine Eingabe erfolgt, und das bisher geschriebene als neues Zeichen interpretiert. (Empfehlung: Einschalten)
• Stifteingabe als Standard setzen: Beim Aufruf wird automatisch der Stifteingabemodus aktiviert (sinnvoll bei Verwendung eines Tablets mit Stift).
• Reaktionszeit: Legt bei Stifteingabe die Zeitspanne fest, nach der die letzte Eingabe als Zeichen interpretiert wird. Kürzere Dauern erlauben flüssigeres Schreiben, erschweren jedoch ggf. die Eingabe von Zeichen wie + oder T, bei der der Stift neu angesetzt werden muss. (Empfehlung: 250 ms)
• Debug Checker, Debug Core und Debug Input: Nur bei der Fehleranalyse durch die Systementwickler von Bedeutung.
• Zwischenfehler speichern: Erlaubt die nachträgliche Analyse von Fehlern durch die Systementwickler und unterstützt so die kontinuierliche Verbesserung des Systems.

Wichtiger Hinweis:
Wenn Sie anstelle der Tastatur die handschriftliche Eingabe (Stifteingabe) nutzen wollen, beachten Sie bitte unbedingt die Informationen zum Handschrift-Training auf der Seite Handschriftliche Eingabe, um eine gute Erkennung Ihrer Handschrift zu erreichen.

→ Kapitelübersicht  → Hauptseite

Brüche

Die Größe von Zeichen kann bei gedrückter Umschalttaste mit Hilfe der Pfeiltasten geändert werden. Durch die Verlängerung wird das Minuszeichen zu einem Bruchstrich:

Beachten Sie bitte, dass Zähler und Nenner immer ganz oberhalb bzw. unterhalb des Striches stehen müssen!

→ Kapitelübersicht  → Hauptseite

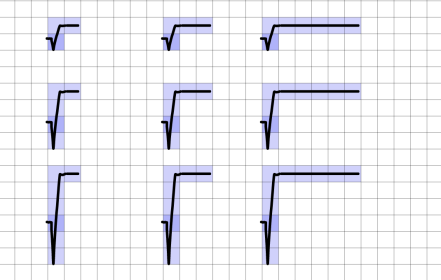
Wurzeln

Wurzeln können in der Größe verändert werden, so dass der Radikand eingeschlossen werden kann.

Dazu werden die Pfeiltasten in Verbindung mit der Umschalt- (Shift-) Taste genutzt:

Änderung der Größe des Wurzelzeichens

→ Kapitelübersicht  → Hauptseite

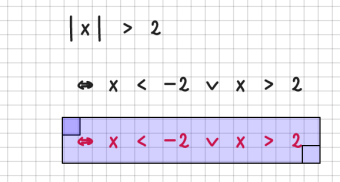
Grenzwerte

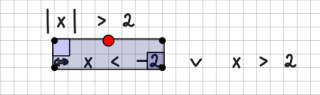
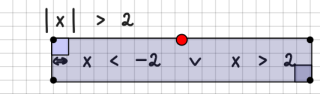
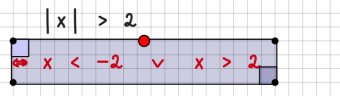
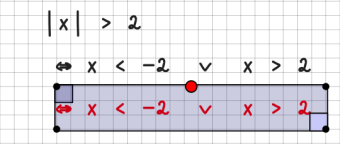
Grenzwerte werden durch lim beschrieben. Achten Sie bitte darauf, dass der Bereich komplett unterhalb von lim steht:

richtig


falsch

→ Kapitelübersicht  → Hauptseite

Integrale

Integrale werden durch int beschrieben. Achten Sie bei bestimmten Integralen bitte darauf, dass die untere und obere Integralgrenze jeweils direkt neben dem Integralzeichen in der untersten bzw. obersten Zeile stehen müssen, und dass zum Integranden eine Leerspalte bleibt:

Beispiele:

1.	richtig
2.	richtig
3.	falsch; die Integralgrenzen stehen in derselben Spalte wie das Integralzeichen
4.	falsch; die Integralgrenzen stehen eine Zeile zu hoch bzw. zu tief
5.	falsch; es fehlt eine Leerspalte vor dem Integranden.

→ Kapitelübersicht  → Hauptseite

Summenzeichen

Das Summenzeichen wird durch sum beschrieben. Achten Sie bitte darauf, dass Start- und Endeangaben für den Summenindex komplett unterhalb bzw. oberhalb des Summenzeichens stehen; ggf. müssen Sie analog zu Wurzeln oder Bruchstrichen das Summenzeichen verbreitern:

 richtig

 falsch

→ Kapitelübersicht  → Hauptseite

Winkelangaben

Winkel können entweder als ^o eingegeben werden, oder in der zweidimensionalen Eingabe als Exponent o:

→ Kapitelübersicht  → Hauptseite

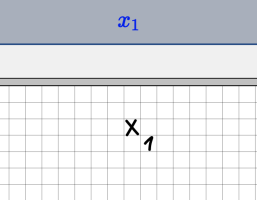
Indexschreibweise

Um einen Index hinzuzufügen, wird dieser um ein Kästchen nach rechts und nach unten versetzt geschrieben:

→ Kapitelübersicht  → Hauptseite

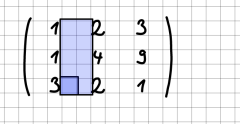
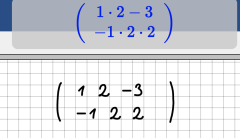
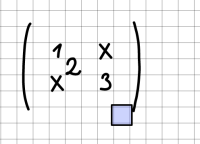
Eingabe von Matrizen

Bei der Eingabe von Matrizen sind die folgenden Punkte zu beachten:

1.	Eine Matrix wird durch eine öffnende und schließende Klammer begrenzt. Die Klammer muss dabei die so groß sein, dass alle Zeilen der Matrix damit abgedeckt werden. Die Größe einer Klammer kann wieder durch die Pfeiltasten (bei gedrückter Umschalttaste) gesteuert werden. Beispiel einer 2x2 Matrix Beispiel einer 3x3 Matrix
2.	Matrixzeilen müssen durch eine Leerzeile getrennt sein. Andernfalls würden die Elemente evtl. als Potenzen oder Indizes erkannt werden. Zwischen den Zeilen muss immer mindestens eine leere Zeile stehen.
3.	Die Elemente einer Spalte müssen untereinander stehen und durch mindestens eine leere Spalte von den anderen Spalten getrennt sein.

Beispiele:

1.	Einträge sind richtig getrennt.
2.	Hier fehlen die trennenden Spalten. Daher wird das Ergebnis als Vektor aufgefasst, in dem 1*2-3  bzw. -1*2*2 steht.
3.	Hier fehlt eine trennende Leerzeile.
4.	Nur das, was innerhalb der Klammern steht, wird auch als Matrix erkannt.

→ Kapitelübersicht  → Hauptseite

Zeile einfügen

Mit der Tastenkombination Umschalt+Eingabe (Shift+Enter) fügen Sie bei einem bestehen Rechenweg eine neue Zeile ein. Die Zeile wird unterhalb der ausgewählten Zeile hinzugefügt.

1.	Kästchen auswählen:
2.	Mit einmaligem Shift+Enter eine Kästchenzeile unterhalb der ausgewählten Zeile eingefügen:
3.	Nach nochmaligem Shift+Enter:

→ Kapitelübersicht  → Hauptseite

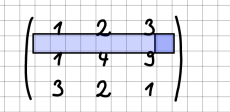
Inhalt auswählen und löschen/kopieren/verschieben

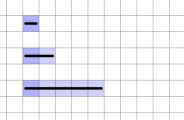
Bei gedrückter linker Maustaste kann durch Ziehen der Maus ein Bereich ausgewählt werden. Der betroffene Inhalt ist schwarz umrahmt und bläulich hinterlegt. Anstelle der Maus können Sie auf einem Tablet auch den Stift nutzen. Wenn Sie weder Maus noch Stift verwenden, können Sie den gewünschten Bereich auch mit den Pfeiltasten bei gleichzeitig gedrückter Umschalttaste markieren.

1.	Oberes linkes Kästchen des zu markierenden Bereichs auswählen:
2.	Linke Maustaste gedrückt halten und Maus nach unten rechts bewegen (oder Stift oder Umschalt- und Pfeiltasten verwenden):
3.	Tasten loslassen bzw. Stift abheben: Bereich ist markiert.

Jetzt haben Sie folgende Möglichkeiten:

1. Mit Backspace wird der ausgewählte Inhalt gelöscht.
2. Mit Strg+c (bzw. command-c) wird der ausgewählte Inhalt kopiert, mit Strg+x (command+x) ausgeschnitten.
3. Anschließend werden mit den Pfeiltasten oder mit Maus/Stift das gewünschte Zielkästchen ausgewählt und mit Strg+v (command+v) der Bereich bzw. eine Kopie dort eingefügt.

Deutlich einfacher und schneller als mittels Kurztasten führen Sie diese Aktionen aus, indem Sie zum Verschieben das untere rechte Kästchen und zum Kopieren das obere linke Kästchen des markierten Bereichs verwenden. An diesem Kästchen ziehen Sie mit Maus oder Stift den Bereich oder ein Duplikat davon an die gewünschte Stelle. Ohne Maus und Stift verwenden Sie hierzu die Pfeiltasten, während Sie die Strg- (bzw. control-) Taste zum Verschieben oder die Alt- (bzw. option-) Taste zum Duplizieren gedrückt halten.

Die nachstehenden Abbildungen skizzieren das beschriebene Vorgehen:

1.	Bereich wurde markiert.
2.	Mit Maus oder Stift wurde in Abbildung 1 das untere rechte Kästchen ausgewählt und bei gedrückter linker Maustaste plus Mausbewegung bzw. mittels Stift nach links gezogen. Alternativ wurden die Pfeiltasten bei gedrückter Strg- (control-) Taste verwendet.
3.	Mit Maus oder Stift wurde in Abbildung 1 das obere linke Kästchen ausgewählt und bei gedrückter linker Maustaste plus Mausbewegung bzw. mittels Stift nach unten gezogen. Alternativ wurden die Pfeiltasten bei gedrückter Alt- (option-) Taste verwendet.

→ Kapitelübersicht  → Hauptseite

undo/redo

Die undo- und redo-Tasten befinden sich in der unteren aufklappbaren Symbolleiste:

undo-/redo-Tasten hier rot umrahmt

Durch Click auf den linken Pfeil (undo) wird die letzte Eingabe rückgängig gemacht. Durch Click auf den rechten Pfeil (redo) wird die in der Eingabehistorie letzte Eingabe wieder dargestellt.

→ Kapitelübersicht  → Hauptseite